浮点精度运算不准确是为什么

这篇文章上次修改于 1354 天前，可能其部分内容已经发生变化，如有疑问可询问作者。

为什么浮点精度运算会有问题

我们平常使用的编程语言大多都有一个问题——浮点型精度运算会不准确。比如

double num = 0.1 + 0.1 + 0.1;
// 输出结果为 0.30000000000000004
double num2 = 0.65 - 0.6;
// 输出结果为 0.05000000000000004

笔者在测试的时候发现 C/C++ 竟然不会出现这种问题，我最初以为是编译器优化，把这个问题解决了。但是 C/C++ 如果能解决其他语言为什么不跟进？根据这个问题的产生原因来看，编译器优化解决这个问题逻辑不通。后来发现是打印的方法有问题，打印输出方法会四舍五入。使用 printf("%0.17f\n", num); 以及 cout << setprecision(17) << num2 << endl; 多打印几位小数即可看到精度运算不准确的问题。

那么精度运算不准确这是为什么呢？我们接下来就需要从计算机所有数据的表现形式二进制说起了。如果大家很了解二进制与十进制的相互转换，那么就能轻易的知道精度运算不准确的问题原因是什么了。如果不知道就让我们一起回顾一下十进制与二进制的相互转换流程。一般情况下二进制转为十进制我们所使用的是按权相加法。十进制转二进制是除2取余，逆序排列法。很熟的同学可以略过。

// 二进制 10010 到十进制
// 从右向左按权相加
10010 = 0 * 2^0 
      + 1 * 2^1 
      + 0 * 2^2 
      + 0 * 2^3 
      + 1 * 2^4 = 18  

// 十进制 18 到二进制
18 / 2 = 9 .... 0 
9 / 2 = 4 .... 1 
4 / 2 = 2 .... 0 
2 / 2 = 1 .... 0 
1 / 2 = 0 .... 1

10010

PS：2^3 代表 2 的三次方，以此类推。

那么，问题来了十进制小数和二进制小数是如何相互转换的呢？十进制小数到二进制小数一般是整数部分除 2 取余数，逆序排列，小数部分使用乘 2 取整数位，顺序排列。二进制小数到十进制小数还是使用按权相加法。

// 二进制 10.01 到十进制的转化
// 从右向左按权相加，小数点后面的从 -1 开始
10.01 = 1 * 2^-2 
      + 0 * 2^-1 
      + 0 * 2^0 
      + 1 * 2^1 = 2.25


// 十进制 2.25 到二进制的转化
// 因为小数和整数计算方法不一样，这里我们需要把小数和整数分开算。
// 整数部分除 2 ，算出的结果继续除 2 ，直至结果为零结束，每一步计算的余数逆序排列
2 / 2 = 1 .... 0
1 / 2 = 0 .... 1

// 小数部分乘 2 ，算出结果的小数部分继续乘 2 ，直至没有小数为止，每一步计算结果的整数部分顺序排列
0.25 * 2 = 0.5 整数部分为 0
0.5 * 2 = 1 整数部分为 1，后面没有小数，计算结束。

// 结果 10.01

转小数我们也了解了，接下来我们回归正题，为什么浮点运算会有精度不准确的问题。接下来我们看一个简单的例子 2.1 这个十进制数转成二进制是什么样子的。

2.1 分成两部分
// 整数部分
2 / 2 = 1 .... 0
1 / 2 = 0 .... 1

// 小数部分
0.1 * 2 = 0.2 整数部分为 0
0.2 * 2 = 0.4 整数部分为 0
0.4 * 2 = 0.8 整数部分为 0
0.8 * 2 = 1.6 整数部分为 1
0.6 * 2 = 1.2 整数部分为 1
0.2 * 2 = 0.4 整数部分为 0
0.4 * 2 = 0.8 整数部分为 0
0.8 * 2 = 1.6 整数部分为 1
0.6 * 2 = 1.2 整数部分为 1
0.2 * 2 = 0.4 整数部分为 0
0.4 * 2 = 0.8 整数部分为 0
0.8 * 2 = 1.6 整数部分为 1
0.6 * 2 = 1.2 整数部分为 1
..... 小数一直不为 0 一直计算下去 .......

继续算下去你会发现小数无限循环结果为 10.0001100110011........ ，但是我们的计算机在存储小数时肯定是有长度限制的，所以会进行截取部分小数进行存储，从而导致计算机存储的数值只能是个大概的值，而不是精确的值。从这里看出来我们的计算机根本就无法使用二进制来精确的表示 2.1 这个十进制数字的值，连表示都无法精确表示出来，计算肯定是会出现问题的。

精度运算丢失的解决办法

现有有三种办法

如果业务不是必须非常精确的要求可以采取四舍五入的方法来忽略这个问题。
转成整型再进行计算。
使用 BCD 码存储和运算二进制小数(感兴趣的同学可自行搜索学习)。

一般每种语言都用高精度运算的解决方法（比一般运算耗费性能），比如 Python 的 decimal 模块，Java 的 BigDecimal，但是一定要把小数转成字符串传入构造，不然还是有坑，其他语言大家可以自行寻找一下。

# Python 示例
from decimal import Decimal

num = Decimal('0.1') + Decimal('0.1') + Decimal('0.1')
print(num)

// Java 示例
import java.math.BigDecimal;

BigDecimal add = new BigDecimal("0.1").add(new BigDecimal("0.1")).add(new BigDecimal("0.1"));
System.out.println(add);

拓展：详解浮点型

上面既然提到了浮点型的存储是有限制，那么我们看一下我们的计算机是如何存储浮点型的，是不是真的正如我们上面提到的有小数长度的限制。
那我们就以 Float 的数据存储结构来说，根据 IEEE 标准浮点型分为符号位，指数位和尾数位三部分（各部分大小详情见下图）。

IEEE 754 标准

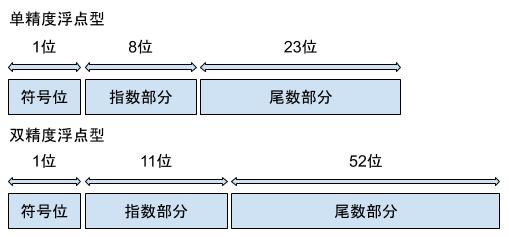
一般情况下我们表示一个很大或很小的数通常使用科学记数法，例如：1000.00001 我们一般表示为 1.00000001 * 10^3，或者 0.0001001 一般表示为 1.001 * 10^-4。

符号位

0 是正数，1 是负数

指数位

指数很有意思因为它需要表示正负，所以人们创造了一个叫 EXCESS 的系统。这个系统是什么意思呢？它规定最大值 / 2 - 1 表示指数为 0。我们使用单精度浮点型举个例子，单精度浮点型指数位一共有八位，表示的十进制数最大就是 255。那么 255 / 2 - 1 = 127，127 就代表指数为 0。如果指数位存储的十进制数据为 128 那么指数就是 128 - 127 = 1，如果存储的为 126，那么指数就是 126 - 127 = -1。

尾数位

比如上述例子中 1.00000001 以及 1.001 就属于尾数，但是为什么叫尾数呢？因为在二进制中比如 1.xx 这个小数，小数点前面的 1 是永远存在的，存了也是浪费空间不如多存一位小数，所以尾数位只会存储小数部分。也就是上述例子中的 00000001 以及 001 存储这样的数据。

我们举个小例子。查看一个单精度浮点型 1.25 的具体存储结构。可以使用以下 Python 代码来查看存储 float 的具体数据结构。

import struct

num = 1.1
bins = ''.join('{:0>8b}'.format(c) for c in struct.pack('!f', num))
print(bins)

Java 版本的代码有点长，我就放个链接了。
Java 版代码链接

IEEE 754 标准

通过上述程序我们得到的存储 1.25 的 float 二进制结构的具体值为 00111111101000000000000000000000 ，我们拆分一下 0 为符号位他是个正值。01111111 为指数位，01000000000000000000000 是尾数。接下来我们验证一下 01111111 转为十进制是 127，那么经过计算指数为 0。尾数是 01000000000000000000000 加上默认省略的 1 为 1.01（省略后面多余的 0），转换为十进制小数就是 1.25。

光明顶的熊